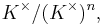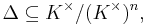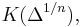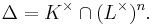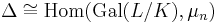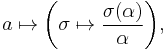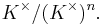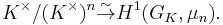Kummer theory

In abstract algebra and number theory, Kummer theory provides a description of certain types of field extensions involving the adjunction of nth roots of elements of the base field. The theory was originally developed by Ernst Eduard Kummer around the 1840s in his pioneering work on Fermat's last theorem. The main statements do not depend on the nature of the field - apart from its characteristic, which should not divide the integer n - and therefore belong to abstract algebra. The theory of cyclic extensions of the field K when the characteristic of K does divide n is called Artin-Schreier theory.

Kummer theory is basic, for example, in class field theory and in general in understanding abelian extensions; it says that in the presence of enough roots of unity, cyclic extensions can be understood in terms of extracting roots. The main burden in class field theory is to dispense with extra roots of unity ('descending' back to smaller fields); which is something much more serious.

1 Kummer extensions
2 Kummer theory
3 Generalizations
4 See also
5 References

Kummer extensions

A Kummer extension is a field extension L/K, where for some given integer n > 1 we have

K contains n distinct nth roots of unity (i.e., roots of Xⁿ-1)
L/K has abelian Galois group of exponent n.

For example, when n = 2, the first condition is always true if K has characteristic ≠ 2. The Kummer extensions in this case include quadratic extensions L = K(√a) where a in K is a non-square element. By the usual solution of quadratic equations, any extension of degree 2 of K has this form. The Kummer extensions in this case also include biquadratic extensions and more general multiquadratic extensions. When K has characteristic 2, there are no such Kummer extensions.

Taking n = 3, there are no degree 3 Kummer extensions of the rational number field Q, since for three cube roots of 1 complex numbers are required. If one takes L to be the splitting field of X³ − a over Q, where a is not a cube in the rational numbers, then L contains a subfield K with three cube roots of 1; that is because if α and β are roots of the cubic polynomial, we shall have (α/β)³ =1 and the cubic is a separable polynomial. Then L/K is a Kummer extension.

More generally, it is true that when K contains n distinct nth roots of unity, which implies that the characteristic of K doesn't divide n, then adjoining to K the nth root of any element a of K creates a Kummer extension (of degree m, for some m dividing n). As the splitting field of the polynomial Xⁿ − a, the Kummer extension is necessarily Galois, with Galois group that is cyclic of order m. It is easy to track the Galois action via the root of unity in front of $\sqrt[n]{a}.$

Kummer theory

Kummer theory provides converse statements. When K contains n distinct nth roots of unity, it states that any cyclic extension of K of degree n is formed by extraction of an nth root. Further, if K^× denotes the multiplicative group of non-zero elements of K, cyclic extensions of K of degree n correspond bijectively with cyclic subgroups of

$K^{\times}/(K^{\times})^n,\,\!$

that is, elements of K^× modulo nth powers. The correspondence can be described explicitly as follows. Given a cyclic subgroup

$\Delta \subseteq K^{\times}/(K^{\times})^n, \,\!$

the corresponding extension is given by

$K(\Delta^{1/n}),\,\!$

that is, by adjoining n^th roots of elements of Δ to K. Conversely, if L is a Kummer extension of K, then Δ is recovered by the rule

$\Delta = K^\times \cap (L^\times)^n.\,\!$

In this case there is an isomorphism

$\Delta \cong \operatorname{Hom}(\operatorname{Gal}(L/K), \mu_n)$

given by

$a \mapsto \biggl(\sigma \mapsto \frac{\sigma(\alpha)}{\alpha}\biggr),$

where α is any nth root of a in L.

Generalizations

There exists a slight generalization of Kummer theory which deals with abelian extensions with Galois group of exponent n, and an analogous statement is true in this context. Namely, one can prove that such extensions are in one-to-one correspondence with subgroups of

$K^{\times}/(K^{\times})^n. \,\!$

If the ground field K does not contain the nth roots of unity, one sometimes still uses the phrase Kummer theory to refer to the isomorphism

$K^{\times}/(K^{\times})^n \stackrel{\sim}{\rightarrow} H^1(G_K, \mu_n). \,\!$

References

Hazewinkel, Michiel, ed. (2001), "Kummer extension", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=k/k055960
Bryan Birch, "Cyclotomic fields and Kummer extensions", in J.W.S. Cassels and A. Frohlich (edd), Algebraic number theory, Academic Press, 1973. Chap.III, pp.85-93.

Kummer theory

Contents

Kummer extensions

Kummer theory

Generalizations

See also

References